Gravity Sim INFO (Documentation)
FONT SIZE
If the default size of this text is difficult to read, you may increase the font size as follows:
- Mac browser: Press [command +].
- Windows browser: Press [Ctrl +].
- Application: Use the Zoom menu.
WHAT NEXT?
After first running the demonstration using the [← Show Me] button at least once, run the simulations in order (from top to bottom) as they appear in the Choose_Simulation↓ menu. Prior to running the Circular orbit simulation, it is critical that you read the WHAT IS IT? section, below, to gain an appreciation for the scientific import of the GravitySim software.
Instead of running the Java applet in your browser, consider downloading the application from the homepage and running it locally on your computer (you will also need to install NetLogo). A major benefit is the ability to use the Zoom menu (not available in the applet) to resize the interface to better fit your monitor, which is advantageous for most laptops. Also, running the application locally provides substantial improvements in graphics resolution and animation quality compared to the applet.
To run a simulation:
- Select a simulation in the Choose_Simulation↓ menu.
- Click [Set Up Simulation].
- Confirm “first time?” query to optimize initial control settings.
- Click [Run Simulation].
- Examine results when the default simulation terminates automatically.
After the default initial simulation:
- Manually alter control settings to investigate their effects.
- Click [Show This Orbit] (only if you change orbits).
- Click [Set Up Simulation] (applies new settings).
- Click [Run Simulation].
SOFTWARE TEST SIMULATION
In the “Software test” simulation, each test mass has an independent initial velocity vector consistent with an ideal circular orbit. The set of three balls in each row (top middle, bottom) are slightly out of phase in what is effectively the same circular orbit. Accordingly, the middle row has the reference orbital period, the top row has a slightly higher orbital radius with a slightly longer orbital period and the bottom row has a slightly shorter orbital radius with a slightly shorter orbital period.
Since the middle row exhibits the same behavior in the dynamical test simulation as seen in the kinematical demonstration ([← Show Me] button), this demonstrates that the dynamical test simulation produces accurate behavior. Moreover, with Synchronous rotation -On-, the linear trajectory of the top and bottom rows provides an extra validation check.
This test simulation is distinctly different from the conventional “Circular orbit” simulation because in the latter simulation the test masses are initially at relative rest, which means that they all share the magnitude and direction of the reference frame’s initial velocity vector. Sensitivity of the dynamical system to initial conditions is made evident by running the “Circular orbit” simulation (after first using the recommended default settings) using the same Orange_Ball_Mass value (1 gram) as the “Software test” simulation. The dynamical behavior of the middle row test masses is markedly different for the two distinct initial conditions.
WHY A “TOY MODEL”?
So-called “toy models” play a very important role in theoretical physics. Their purpose is to demonstrate, in a simple and direct way (typically by eliminating extraneous complexity), fundamental physical principles at work in real, complex physical systems. For example, an apple falling from a tree, which simply demonstrates gravitational attraction, is a “toy model” of astrophysical gravitation between planets, moons, stars and galaxies. Isaac Newton was the first person to understand that astrophysical gravity and local gravity, which causes objects to fall to Earth, are the identical physical phenomenon. According to Stukeley’s account, Newton had this revolutionary thought (circa 1665 at Woolsthorpe Manor) only after watching an apple fall from a tree; in effect, the apple tree, which gave the apple its initial gravitational potential, was Newton’s serendipitous “toy model.”
The behavior of the test particles shown in the GravitySim software simulations is not subject to dispute because no disputable assumptions are being made; one simply observes the basic dynamical results of Newton’s Law of Gravity. Similar to the eight 1-gram test particles in the simulation, which do not self-interact, there is essentially no interaction between individual stars in a galactic disk because they are generally too far apart for the gravitational fields of neighboring stars to affect each other. Instead, the orbital motion of stars in the disk, having a period on the order of 100 Myr, is a response to the collective mass of the host galaxy, with the majority of this mass being restricted to the region of the galactic nucleus. In hindsight, it is obvious that the dynamical behavior of these stars must also be influenced by the collective mass of any neighboring galaxies; a co-orbiting galaxy pair or a galaxy orbiting a cluster barycenter may be quite widely separated so that they exhibit no immediate visual relationship as compared to overtly interacting galaxies.
The following schematic of an inertial frame of reference (square) in an idealized circular orbit around a similarly-idealized ‘point mass’ (blue sphere) is a vast simplification of the actual, extremely complex dynamical system of co-orbiting cluster galaxies (also see WHAT IS IT?). However, the basic principles of Newton’s Law of Gravity clearly apply. The point of using such a “toy model” as the subject of a simulation is to investigate the fundamental dynamical effects of the inverse square law on the stars in the spiral galaxy’s disk. It proves to be the case that these effects are not theoretically obvious, although they are empirically obvious, which means that the empirical observation is subject to incorrect initial interpretation, which is precisely what occurred about thirty-five years ago.

Fundamental physical principles that are clearly and demonstrably true for a few, tiny particles orbiting the Earth (in a simple, virtual “toy model”) can be extrapolated to real stars in an actual galactic disk because both dynamical systems are subject to the same immutable, mathematically-defined physical laws operating at different scales. Moreover, the simple GravitySim dynamical model makes it patently clear that conventional digital simulations of spiral galaxy formation that do not take into account the long-term gravitational effects of the environment, out to a distance of at least several million light years, cannot accurately reflect empirical reality; ignoring the gravitational effects of neighboring galaxies on the evolutionary internal dynamics of spiral galaxies is obviously naïve.
WHAT IS IT?
The fundamental purpose of the GravitySim[ulator] software is to address the issue discussed in the following paragraph quoted verbatim from {James Binney and Michael Merrifield Galactic Astronomy (Princeton University Press, 1998), pp. 19–20.} This textbook from the eight-volume Princeton Series in Astrophysics, edited by Jeremiah Ostriker & David Spergel, is a current standard reference in professional astronomy and astrophysics. Both editors are prominently featured in the BBC HORIZON documentary linked in the VIDEOS section, below.
Since it is the gravitational pull of a galaxy that provides the force which retains the gas on its approximately circular orbits, it is straightforward to translate the observed orbital velocities in a gas disk into an estimate of the distribution of mass in the galaxy. We can compare the mass derived in this way to the sum of the masses of the individual components such as the stars in the disk and spheroid, and the hydrogen gas itself. The surprising result of such comparisons in the 1970s was that the total mass inferred dynamically exceeds the sum of all the known components, and that the discrepancy becomes greater as we look to larger radii in a galaxy. From these observations it was inferred that galaxies are embedded in huge dark halos, which contain considerably more mass that the visible galaxies themselves. This unexpected discovery was originally dubbed the “missing mass problem”, but this title is somewhat confusing, since we know from the kinematics that there is an excess of mass rather than a deficit. The real problem is that we do not know what form the excess mass takes, since it evidently is not made up of directly-visible material. Our inability to identify the nature of the material which dominates the mass of many systems is therefore now usually referred to as the “dark matter problem.” Its resolution remains one of the major goals of galactic astronomy.
The following graph is sourced from the University of Sheffield Dark Matter Research website, which includes this quotation:
“Attempting to solve the dilemma of whether dark matter exists and, if so, what it
consists of is of great importance to the scientific world.” (November 2012)
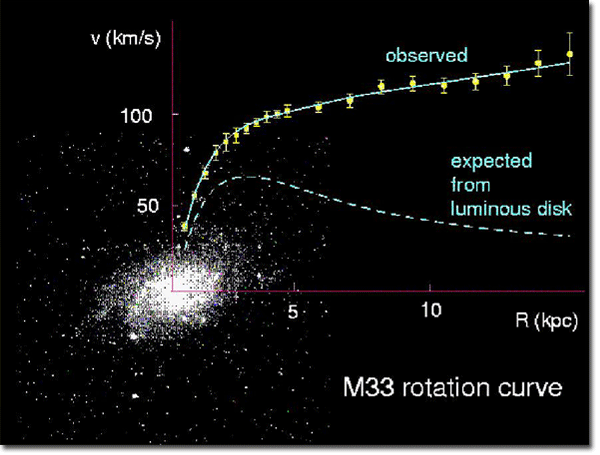
A kiloparsec (kpc) is about 3,262 light years. Note the approximately-constant, positive slope of the empirical v(R) function for R > 5 kpc; ‘particles’ at greater radius apparently orbit at higher velocity. Upon consideration, an external gravitational source (i.e., a remote galaxy) may induce positive radial motion in addition to the locally-induced orbital motion. If such an outflow exists, then observations imply that the orbital motion of the particles is accelerating as they move radially outward. Accordingly, if a similar relationship is seen in the GravitySim graph (Speed Relative to Reference Frame Centroid), showing orbital velocity acceleration that is approximately constant over R, this means that the simulation is predicting the same behavior that is observed empirically. (Look for it in the Circular orbit simulation.)
The orbital period of stars moving at ~100 km/s in an approximately-circular orbit at a radius of 5 kpc is ~300 million years. Accordingly, assuming a static galactic orbital radius of ~5 kpc, a star that is about ten billion years old in such an orbit has made over thirty complete circuits of the host galaxy over its lifetime and even more if it has undergone radial migration. It is then clear that the orbital motion of stars, per se, is not responsible for the appearance of spiral galaxies, whose arms exhibit a spiral morphology consistent with an apparent winding number that is typically less than two revolutions.
The GravitySim software provides a virtual laboratory that demonstrates the effect of an idealized, static, spherically-symmetric, point-mass gravitational field on non-self-interacting, small, 1-gram test particles (i.e., it demonstrates Newton’s [inverse square] Law of Gravity). Gravity is difficult to study empirically because it cannot be neutralized and because it is weak in comparison to electromagnetic forces. The idealized laboratory of the computer produces accurate modeling of fundamental physical principles (i.e., a realistic, virtual “toy model”), which reveals unintuitive dynamical behavior in response to a gravitational field.
“Dark matter is such a fundamental problem now, within both physics and cosmology,
that finding the answer to that problem is going to be an enormous discovery.”
– Prof. Timothy Sumner, Imperial College London (2006)† [See VIDEOS.]
Beyond any reasonable doubt, the simulation reveals that the “excess mass” required to explain the empirical observations typified by the foregoing graph exists external to the observed galaxy in the form of at least one additional galaxy or, more typically, the barycenter of a group of galaxies. The observed dynamical behavior of stars in galaxy disks, which is very different from the orbital motion of the planets, is due to the simple fact that the former is subject to external gravitational fields (i.e., other galaxies), while the latter is not subject to external gravitational fields (i.e., other stars). The Solar System is a dynamical system dominated by Solar gravity because the Sun contains about 99.98% of the total mass. Furthermore, it is ‘isolated’ from gravitational interaction with other individual stars because the nearest stars are very distant as compared to the effective radius of the Solar System. The nearest star to the Sun, Proxima Centauri, is about 9,000 times the distance between the Sun and Neptune. The Galactic center (Sagittarius A*), which marks the effective center of the Sun’s approximately-circular Galactic orbit, is about 6,500 time farther, which is nearly 60 million times the distance between the Sun and Neptune. As concerns the Sun’s Galactic orbit, this distance is offset by the fact that it represents an effective Newtonian ‘point-mass’ on the order of 100 billion solar masses.
Galaxies, which are grouped in clusters, are not similarly isolated, so their internal dynamics are very much affected by gravitational interaction with neighboring galaxies. As a collection of gravitationally-bound stars, every spiral galaxy (and all of its individual component stars) participate in a dynamical gravitational system, which includes other galaxies. This is made clear by images of distant galaxy clusters, for example this Hubble Space Telescope (HST) image of an exceptionally rich galaxy cluster, Abell 1689. This image, which is about 3.2 arcminutes in diameter, makes it immediately obvious that, relative to their size, neighboring galaxies in clusters are not far apart; small galaxy separations appear to be within about ten extended galactic radii and large separations within the main population are certainly within several hundred galactic radii, where the average diameter of the typical galaxies shown here is understood to be similar to the Milky Way, or on the order of 100,000 light years.

No ‘dark halo,’ ostensibly made up of mysterious particles other than atoms, which produce gravity, yet have no radiation signature whatsoever, is necessary to explain spiral galaxy rotation curves. It was a longstanding mistake to assume that the additional mass required to explain internal spiral galaxy dynamics had to exist internal to a boundary centered on and local to the galaxy whose rotation curve was measured (e.g., M33). In order for such a measurement to be made, the target has to be relatively close, which means that it generally fills the telescope’s field of view, as is the case for the following image of M33, which is about 80 arcminutes in diameter. The yellow square in the upper left-hand corner shows the relative size of the HST image of Abell 1689, above. The common idiom, “out of sight, out of mind” is applicable to the neighboring, co-orbiting galaxies of any single target galaxy observed in a telescopic image. The gravitational fields of these co-orbiting galaxies, which are typically not visible in the target image, certainly affect the systemic motion of the target galaxy within its host cluster, as well as the individual dynamics of its constituent stars.

The alleged particles making up the inferred “dark halo” around spiral galaxies are undetectable for the simple reason that they need not exist to explain spiral galaxy rotation curves, and clearly do not exist. It is certainly true that an additional gravitational force (necessarily produced by a considerable mass in addition to that of the target galaxy) is needed to account for observed spiral galaxy rotation curves, yet the same observations imply that this mass cannot possibly be collocated with the target galaxy. The internal dynamics of a spiral galaxy (i.e., its rotation curve) is quite obviously affected by dynamical interaction with external galaxies, which may be far outside the telescope’s field of view when a spectrograph is used to measure the rotation curve of a typical target galaxy.
The following quotation from {J. Binney & M. Merrifield, op. cit., pp. 227–228} is particularly relevant to what one sees in the default Circular orbit simulation. This simulation shows that the spiral-galaxy “dark matter problem” and the “winding problem” are related, and definitively solves both of these astrophysical problems. It reveals that the astrophysics community came close to an understanding of observed phenomena, yet a few key ideas required to correct erroneous conventional thinking were missing, which is generally the case in the history of scientific progress.
…it follows that spiral structure is not an entirely gas-dynamic phenomenon, which leaves the bulk of the mass in the disk quite unmoved. Instead it must be associated with some sort of gravity wave that propagates through the stellar disk.
Finally, the minima in the amplitudes of the arms as a function of azimuth have been convincingly interpreted as nodes in the interference pattern of two spiral waves, a dominant trailing wave and a subordinate leading wave (Toomre 1981). That is, at the minima, a trough of the leading wave crosses the peak of the trailing wave, partially canceling it. In this picture the disk forms a resonant cavity within which energy is carried in and out by leading and trailing spiral waves.
It is thought that grand-design spiral structure is usually generated by either a rotating bar within the galaxy (see below) [“below” reference not quoted here], or by the tidal gravitational field of a companion galaxy. In the case of M51, the perturbing companion, NGC [5195] is clearly visible to the North in Figure 4.55.
In the GravitySim software, the same set of iterated instructions (see “HOW IT WORKS”) produce all of the simulated physical phenomena. The initial simulation, Radial free fall, exhibits well-known behavior (i.e., the “spaghetti effect”) associated with both radial and horizontal gravitational tidal forces. The second simulation, Software test, is described in a special section of this document, above. The third simulation, Circular orbit, exhibits unintuitive dynamical behavior caused by time variation (integrated over a circular orbit) of the same unequal force vectors that produce the spaghetti effect. This simulation resolves the spiral-galaxy “dark matter problem” as evinced by the graphed linearly-increasing velocity of the test particles as a function of the radial coordinate. This is the same behavior graphed above in the empirical M33 rotation curve (“observed”) for R > 5 kpc. This simulation also resolves the winding problem as evinced by the morphology produced by the dynamics over time and the correspondence of the simulated dynamical process to the foregoing theoretical description of the fundamental physical process necessary to produce the observed spiral structures.
The two remaining two simulations, Match the image and Empty space, are self explanatory when they are run. The former relates to the cosmological implications of the new, corrected understanding of spiral galaxy evolutionary dynamics, while the latter is included as a visual verification test for the dynamical simulation software, which produces all of the simulations using the identical process (i.e., set of iterated software routines).
HOW IT WORKS
The simulations are produced by a simple procedure; see the inline comments in the 6-line “physics-0-sequence” routine in the software code, which can be reviewed via the < Code > link at the top of this page. This routine prominently appears at the beginning of the physics section, which immediately follows the initial variable definitions section. This same routine produces all of the dynamical simulations, simply by altering initial conditions.
The key advantage of an idealized circular orbit is that the angular position of the spacecraft in time is known with complete precision in terms of a fraction of the orbital period; therefore, solving Kepler’s Equation of elliptical motion is not required. Another advantage is that the gravitational potential at the centroid of the reference frame is constant. Modeling the source mass as an idealized ‘point mass,’ all that is required is calculation of local gravitational acceleration (i.e., the inverse square law) to high accuracy. The NetLogo math engine underlying the GravitySim software employs double-precision (64-bit) floating point numbers as defined in the IEEE 754 standard (binary64), which allows for approximately 16 decimal digits of calculation precision.
Simulations yield a double integral of gravitational acceleration (GM/R 2) over time, with the first integration yielding change in velocity (dv = ∫a∙dt) and the second integration yielding change in spatial position (ds = ∫v∙dt).
The ||Simulation_Interval slider control is the “variable of integration” (dt); for practical reasons, it cannot be arbitrarily small, in contrast to the ideal mathematical case. A smaller dt value yields a more accurate simulation (i.e., integral approximation) at the expense of the speed at which the computer can produce the simulation. Although a larger value of dt, yielding a faster simulation, technically produces a less-accurate simulation, there is generally no noticeable difference in modeled behavior. This is because modeling errors are already very small for maximum available values of dt.
HOW TO USE IT
See the WHAT NEXT? section, above, for basic instructions.
The controls are generally self-explanatory. See HOW IT WORKS, above, for information on the ||Simulation_Interval slider.
Trace Controls have no physical effect on the simulation; these controls only affect how often the test-mass position trace dots are produced in terms of simulated real time.
THINGS TO NOTICE
The dots tracing the dynamical behavior of the orbiting test masses are equally spaced in simulated real time according to the ||Trace_Interval slider-control setting. Thus, in addition to the dynamic graph (Speed Relative to Reference Frame Centroid), acceleration is visually indicated by increasing distance between successive dots. Also, the general message box (lower right) provides quantitative analysis of the velocity trend over time and distance.
VIDEOS
CONFRONTING THE UNIVERSE: Is dark matter real? (Nature Video, 2012).
This documents a brief conversation at the [June] 62nd Annual Lindau Meeting in which Martinus Veltman states, “I think it [dark matter] doesn’t exist.” (@ timecode 4:35)
† Most of the Universe is Missing (BBC Horizon, 2006).
A description of ‘dark matter’ as quoted in the second documentary (@ timecode 2:14):
“It’s not physics, OK? — It’s fairies at the bottom of the garden.”
– Prof. Michael J. Disney, Cardiff University
HOW TO CITE
If this model is mentioned in an academic publication, please include these citations for the model, itself, and for the underlying NetLogo environment:
- Mayer, Alexander F. (2012). GravitySim. http://GravitySim.net
- Wilensky, U. (1999). NetLogo. http://ccl.northwestern.edu/netlogo/
Center for Connected Learning and Computer-Based Modeling,
Northwestern University, Evanston, IL.
ACKNOWLEDGEMENTS
I thank Cdr. Louis J. Fabbri, USN (Ret.), for valuable comments concerning the correlation of observed simulated gravitational tidal effects with typical spiral galaxy morphology and for testing and criticism of interface development.
I thank Tadeusz Glinkiewicz for general discussion concerning software development.
I thank Uri Wilensky, Director of The Center for Connected Learning and Computer-Based Modeling at Northwestern University, for the NetLogo development environment.
I thank various engineering teams at Apple Computer, Adobe Systems and Google for providing additional technical resources that were essential for this project.
COPYRIGHT
Copyright © 2012–2013 Alexander Franklin Mayer.



